VAR
a: ARRAY[10,15] OF LONG;
b: ARRAY[5] OF INTEGER;
m,n: INTEGER;
s: LONG
...
IF NOT( (m>n) OR (m>5) ) THEN
s := a[b[m],n];
ELSE
n := b[m-5];
END
|
Erzeugen Sie für das rechte Programmstück Quadrupel-Code nach der
Kontrollflussmethode. Ein INTEGER ist 4 Byte und ein
LONG 8 Byte groß. Die Untergrenze aller Indexbereiche ist 0.
Zur Beachtung: Zu Beginn wird kein Label erzeugt. Das
NOT in der Bedinung dreht nur die schon erzeugten Labels um.
Die offenbar überflüssigen gotos und Labels dürfen nicht
entfernt werden.
if m>n goto IFfalse goto ORfalse ORfalse: if m>5 goto IFfalse goto IFtrue IFtrue: t1 = m * 4 t2 = t1 + adr(b) t3 = @t2 t4 = t3 * 15 t5 = t4 + n t6 = t5 * 8 t7 = t6 + adr(a) t8 = @t7 s = t8 goto IFend IFfalse: t9 = m - 5 t10 = t9 * 4 t11 = t10 + adr(b) t12 = @t11 n = t12 IFend:
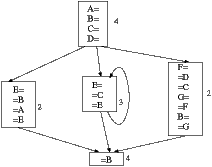
Gegeben sei der folgende Kontrollflussgraph. Rechts von den Blöcken sind die erwartetend Ausführungshäufigkeiten angegeben.
a) Geben Sie den Konfliktgraphen und die Auslagerungskosten für alle Pseudoregister an - dabei soll angenommen werden, dass ein Speicherbefehl zwei Zyklen und ein Ladebefehl drei Zyklen kosten soll.
b) Bestimmen Sie eine Reihenfolg der Registerbelegung, belegen Sie die Pseudoregister mit realen Registern und kennzeichnen Sie eventuell auszulagernde Pseudoregister. Nehmen Sie an, dass vier reale Register zur Verfügung stehen.
Für den Konfliktgraphen braucht man zuerst die Aktivitätsbereiche der Register.
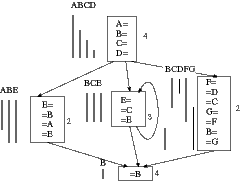
Beachten Sie dabei das Register für B. B wird im
obersten Block beschrieben und im untersten Block gelesen. Aus diesem Grund
muss dieses Register im gesamten Bereich des linken und des mittleren
Blocks aktiv bleiben auch wenn dort nie auf B zugegriffen
wird. Im rechten Block wird hingegen B erneut beschrieben. Der
frühere Wert wird also gar nicht verwendet. Dadurch kann das Register für
B auch anderwertig belegt werden. Es ist nicht überall aktiv.
Durch die Schleife im mittleren Block muss C dauernd aktiv
sein. Der Wert muss ja auch bei einem weiteren Durchlauf der Schleife noch
immer den richtigen Wert haben.
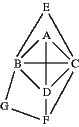
Der Konfliktgraph hat dadurch dieses Aussehen:
Die Auslagerungskosten sind
| R= | =R | Kosten | |
|---|---|---|---|
| A | 4 | 2 | 4*2+2*3=14 |
| B | 6 | 6 | 6*2+6*3=30 |
| C | 4 | 5 | 4*2+5*3=23 |
| D | 4 | 2 | 4*2+5*3=14 |
| E | 5 | 5 | 5*2+5*3=25 |
| F | 2 | 2 | 2*2+2*3=10 |
| G | 2 | 2 | 2*2+2*3=10 |
Die Knoten G, F und E haben alle weniger als vier Kanten und können dadurch zuerst entfernt werden. Die Reihenfolge ist prinzipiell egal. Auch die restlichen Knoten können in beliebiger Reihenfolge entfernt werden weil die Anzahl der Kanten kleiner als vier ist. Wir wählen die Reihenfolge D, C, B und A.
Die Registerbelegung geschieht in umgekehrter Reihenfolge. Für A bis D also die Register 1 bis 4. Für E bleibt dadurch nur Register 4 übrig. Für F kann 1 oder 2 gewählt werden und für B 1 oder 3.
| Reihenfolge | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| Register | 1 | 2 | 3 | 4 | 4 | 2 | 1 |
Gegeben sei folgende Grammatik (Kleinbuchstaben und Sonderzeichen sind Terminalsymbole):
X → L R R → + L R R → ε L → E L → [ E , L ] E → a E → [ L ]
a) Bestimmen Sie die First- und Follow-Mengen für alle Nonterminale der Grammatik.
b) Ist die Grammatik LL(1)? Begründung!
| First | Follow | |
|---|---|---|
| X | [ a | $ |
| L | [ a | + ] $ |
| R | + | $ |
| E | [ a | + , ] $ |
Die Grammatik ist nicht LL(1) weil Bedingung 1 für LL(1)-Grammatiken
verletzt ist. Für die Alternativen αi der Produktionen für
jedes N muss gelten
First(αi) ∩ First(αj) = {} f.a. i, j (i≠j)
Für die Alternativen der Produktion für L gilt das jedoch
nicht:
L → E L → [ E , L ]
| αi | First |
|---|---|
| E | [ a |
| [ E , L ] | [ |
First(E) ∩ First([ E , L ]) = {[} ≠ {}, d.h. die Grammatik ist nicht LL(1).
|
B → GL GL → ( G ) OF | ( G ) OF GL G → O | O G O → k | q | p OF → F | ε F → g | f |
Ein Bild besteht aus Objekten die in Gruppen zusammengefasst sind. Es gibt kugeln, quader und pyramiden mit Breite, Höhe und Farbe. Hinter jeder Gruppe können auch optionale Filter stehen (größen- oder farbänderung) die die Objekte in einer Gruppe verändern. In den Attributen b, h und f eines Objekts stehen Breite, Höhe und Farbe. In g.w bzw. f.w steht der Wert des Filters.
Erweitern Sie die Grammatik um Attribute zur Ausgabe einer Objektliste bei der alle vorhandenen Filter auf die Objektgruppen angewendet wurden und die im Attribut B.x geliefert werden soll, d.h., die gruppierten Objekte sollen aufgeflacht werden. Jedes Objekt wird als Struktur in der Form (objekt, breite, höhe, farbe) ausgegeben. Bei einer Größenänderung werden Breite und Höhe des Objekts mit g.w multipliziert. Bei einer Farbänderung ergibt sich die neue Farbe des Objekts durch die Funktion neu = farbe(alt, f.w). Der Operator & hängt Zeichenketten und Zahlen aneinander.
Beispiel: Aus der Eingabe (q) (p k) g mit den Attributen q.b=1, q.h=2, q.f=3, p.b=2, p.h=1, p.f=6, k.b=2, k.h=4, k.f=9 und g.w=2 wird (q, 1, 2, 3) (p, 4, 2, 6) (k, 4, 8, 9) erzeugt. Der Wert des Größenfilters wurde dabei auf Pyramide und Kugel angewendet.
| B → GL | B.x = GL.x |
| GL → ( G ) OF | GL.x = G.x; G.f = OF.f; G.w = OF.w |
| GL → ( G ) OF GL | GL0.x = G.x & GL1.x; G.f = OF.f; G.w = OF.w |
| G → O | G.x = '(' & O.x & ')'; O.f = G.f; O.w = G.w |
| G → O G | G0.x = '(' & O.x & ')' & G1.x; O.f = G0.f; O.w = G0.w |
| O → k | if( O.f == 'g' ) { O.x = 'k' & k.b * O.w &
k.h * O.w & k.f } else if( O.f == 'f' ) { O.x = 'k' & k.b & k.h & farbe(k.f, O.w) } else { O.x = 'k' & k.b & k.h & k.f } |
| O → q | if( O.f == 'g' ) { O.x = 'q' & k.b * O.w &
k.h * O.w & k.f } else if( O.f == 'f' ) { O.x = 'k' & k.b & k.h & farbe(k.f, O.w) } else { O.x = 'k' & k.b & k.h & k.f } |
| O → p | if( O.f == 'g' ) { O.x = 'p' & k.b * O.w &
k.h * O.w & k.f } else if( O.f == 'f' ) { O.x = 'k' & k.b & k.h & farbe(k.f, O.w) } else { O.x = 'k' & k.b & k.h & k.f } |
| OF → F | OF.f = F.f; OF.w = F.w |
| OF → ε | OF.f = ''; OF.w = 0 |
| F → g | F.f = 'g'; F.w = g.w |
| F → g | F.f = 'f'; F.w = f.w |
Diese Musterlösung ist auch als PDF-Datei verfügbar.