Erzeugen Sie für den folgenden Zwischencode-Baum optimalen Maschinencode für den 68000, wobei das Ergebnis in einem Datenregister landen soll. Verwenden Sie dazu die im Skriptum angegebene Befehlsauswahl-Baumgrammatik. (Optimaler Code hat in erster Linie die geringsten Kosten, inzweiter Linie die geringste Anzahl Befehle.)
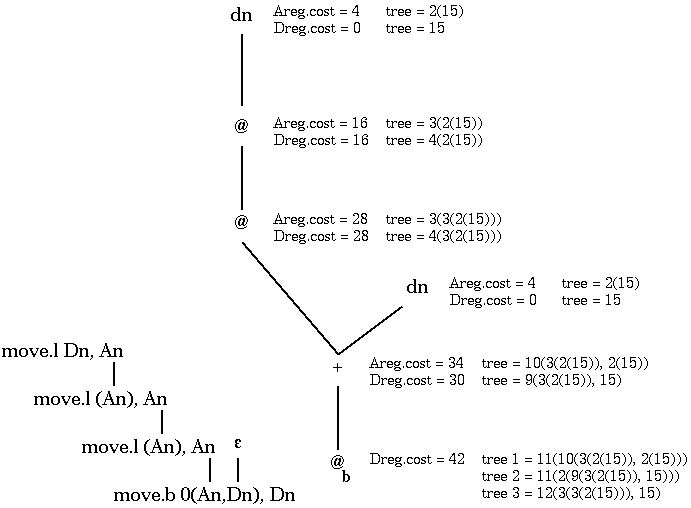
Mit Hilfe der Baumgrammatik aus dem Kapitel "Codeerzeugung" des Skriptums muß man für jeden Knoten des Zwischencode-Baumes die Ableitung mit den geringsten Kosten finden. Treten bei der Berechnung mehrere Ableitungen mit gleichen Kosten auf dann nimmt man diejenige mit der geringeren Befehlsanzahl. Bei gleicher Befehlsanzahl kann man beliebig wählen. Man muß also immer alle Ableitungen in einem Knoten finden damit man überhaupt den optimalen auswählen kann.
Wenn man bei der Ableitung auf eine Befehlskombination stößt, die schon weiter oben berechnet wurde dann kann die Ableitung abgebrochen werden weil damit feststeht, daß eine optimale Befehlskombination gefunden wurde.
Die Ableitung geschieht sowohl für ein Datenregister als auch für ein Adressenregister. Ausgenommen davon ist in diesem Beispiel der letzte Knoten weil ja das Ergebnis laut Angabe in einem Datenregister erwartet wird.
Wir gehen bei der Ableitung von oben nach unten vor. Der erste Knoten hat den Inhalt dn. Für die Ableitung in ein Datenregister erhalten wir daher sofort die Regel 15 mit den Kosten 0. Soll das Ergebnis in einem Adressenregister stehen dann müssen wir die Regel 2 (Areg->Dreg) anwenden. Der Baum ist also 2(15) mit den Kosten 4.
Für den nächsten Knoten müssen wir eine Ableitung für die Zwischencodefolge
dn, @
finden. Für den Knoten @ kommen folgende Regeln in Frage:
Regel 3: Areg -> @(Areg), Kosten 12
Regel 4: Dreg -> @(Areg), Kosten 12
Der einzige Unterschied zwischen diesen beiden Regeln ist das Register für das Ergebnis. Als Parameter wird jeweils ein Adressenregister erwartet. Um ein Datenregister in ein Adressenregister zu bringen kommt nur die Regel 2 in Frage. Von dieser wissen wir aber schon, daß sie optimalen Code erzeugt (siehe oben) und damit können wir sofort die gewünschten Ableitungsäume bilden.
Areg.cost = 16, Areg.tree = 3(2(15))
Dreg.cost = 16, Dreg.tree = 4(2(15))
Als nächstes kommen die Ableitungen für die Codefolge
dn, @, @
Die Regeln für den Knoten @ kennen wir schon. Wir haben auch gesehen, daß diese Regel als Parameter immer ein Adressenregister erwartet. Die einzig möglichen Ableitungsbäume lauten daher
Areg.cost = 28, Areg.tree = 3(3(2(15)))
Dreg.cost = 28, Dreg.tree = 4(3(2(15)))Etliche Leute haben bei der Prüfung fälschlicherweise den Baum Dreg.tree = 4(4(2(15))) als Lösung angegeben. Die Regel 4 liefert jedoch ein Datenregister zurück und kann in diesem Fall daher nicht als Parameter verwendet werden.
Der nächste Knoten wird schon etwas komplizierter. Die Zwischencodefolge lautet
(dn, @, @), dn, +
also eine Addition von @(@(dn)) und einem weiteren Datenregister. Für die Addition gibt es in der Baumgrammatik die folgenden Regeln:
Regel 5: Dreg -> +(Areg,Dreg), Kosten 8
Regel 6: Dreg -> +(Dreg,Dreg), Kosten 8
Regel 7: Areg -> +(Dreg,Areg), Kosten 8
Regel 8: Areg -> +(Areg,Areg), Kosten 8
Regel 9: Dreg -> +(@(Areg),Dreg), Kosten 14
Regel 10: Areg -> +(@(Areg),Areg), Kosten 14
Soll das Ergebnis in einem Datenregister zu stehen kommen dann reduziert sich die Anzahl auf die Regeln 5, 6 und 9. Regel 5 bzw. 6 ergibt die Ableitung 5(3(3(2(15))),15) bzw. 6(4(3(2(15))),15) mit 36 als Kosten.
Verwendet man jedoch die Regel 9 dann kann man sich ein @ ersparen. Die Ableitung lautet 9(3(2(15)),15), hat die Kosten 30 und ist damit die optimale Befehlsfolge an dieser Stelle.
Die Ableitung für das Ergebnis im Adressenregister erfolgt nach dem gleichen Muster. Die Kosten dafür sind etwas höher weil auf jeden Fall ein Datenregister in ein Adressenregister umkopiert werden muß, z.B. erlaubt Regel 10 als Parameter nur Adressenregister. Die optimalen Ableitungsbäume lauten also
Areg.cost = 34, Areg.tree = 10(3(2(15)),2(15))
Areg.cost = 34, Areg.tree = 2(9(3(2(15)),15))
Anmerkung: Von diesen beiden Bäumen können wir willkürlich eine auswählen weil beide die gleichen Kosten und die gleiche Anzahl Befehle haben. Aus ästhetischen Gründen wählen wir die erste Variante.
Dreg.cost = 30, Areg.tree = 9(3(2(15)),15)
Endlich sind wir beim letzten Knoten angelangt. Uns fehlt nur noch die Ableitung von
(dn, @, @), dn, +, @b
Für @b gibt es nur die Regeln
Regel 11: Dreg -> @b(Areg), Kosten 8
Regel 12: Dreg -> @b(+(Areg,Dreg)), Kosten 14
Regel 13: Dreg -> @b(+(Areg,Areg)), Kosten 14
Aufgrund unserer Erfahrung wissen wir, daß uns Regel 13 sicher teuerer kommen wird weil ein Parameter der Addition auf jeden Fall von einem Datenregister in ein Adressenregister umkopiert werden müßäte. Wir werden uns daher auf Regel 11 und 12 beschränken.
Regel 11 erwartet als Parameter ein Adressenregister, d.h., die vorangegangene Addition muß ihr Ergebnis dort zur Verfügung stellen. Damit kommen wir in die gleiche Ableitung wie vorher und können deshalb die Berechnung abbrechen. Wir stellen einfach dem dortigen Ergebnis für das Adressenregister die Regel 11 voran, addieren die zusätzlichen Kosten und erhalten 42. (Jede Ähnlichkeit mit der ultimativen Antwort ist natürlich rein zufällig, also don't panic!)
Regel 12 sieht etwas vielversprechender aus. Bei diesem Befehl ist die Addition von einem Adressenregister und einem Datenregister schon enthalten. Wir können also die Addition überspringen und kommen in die Ableitung von @. Leider kostet Regel 12 soviel, daß sich die Gesamtkosten leider nicht reduzieren. Als Ergebnis erhalten wir diese Regeln mit den selben Kosten:
Dreg.tree1 = 11(10(3(2(15)),2(15)))
Dreg.tree2 = 11(2(9(3(2(15)),15)))
Dreg.tree3 = 12(3(3(2(15))),15)
Der dritte Baum hat um einen Befehl weniger als die anderen beiden. Die optimale Befehlsfolge lautet daher
move.l Dn,An move.l (An),An move.l (An),An move.b 0(An,Dn),Dn