2. Beispiel: Konfliktgraph und Auslagerungskosten

• Angabe
• Lösung
• Erklärung
  • Erstellung des Konfliktgraphen
  • Berechnung der Auslagerungskosten
  • Reihenfolge der Registerbelegung
  • Registerzuteilgung auf reale Register

Angabe

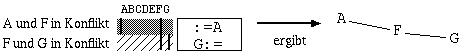
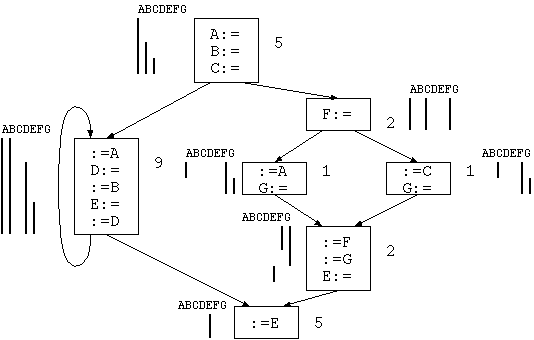
Gegeben sei der folgende Kontrollflußgraph. Neben den Blöcken sind die Aktivitätsbereiche der Pseudoregister und die erwarteten Ausführungshäufigkeiten angegeben.

a)

Geben Sie den Konfliktgraphen und die Auslagerungskosten für alle Pseudoregister an. Dabei soll angenommen werden, daß eine Zuweisung (R:=) einen Zyklus und eine Verwendung (:=R) zwei Zyklen kostet.

b)

Bestimmen Sie eine Reihenfolge der Registerbelegung. Belegen Sie die Pseudoregister mit realen Registern und kennzeichnen Sie die auszulagernden Pseudoregister. Nehmen Sie an, daß drei reale Register zur Verfügung stehen.

Lösung

a) Konfliktgraph und Auslagerunskosten

Konfliktgraph

Auslagerungskosten

R| R:=| :=R|Summe
-+----+----+---------------
A|  5 | 10 | 25 =  5 + 10*2
B|  5 |  9 | 23 =  5 +  9*2
C|  5 |  1 |  7 =  5 +  1*2
D|  9 |  9 | 27 =  9 +  9*2
E| 11 |  5 | 21 = 11 +  5*2
F|  2 |  2 |  6 =  2 +  2*2
G|  2 |  2 |  6 =  2 +  2*2

b) Registerbelegung

Reihenfolge von links nach rechts

A B D E C F G
1 2 3 * 3 2 1

Das Register E muß ausgelagert werden. Anmerkung: Die obige Reihenfolge der Registerbelegung ist nur eine von mehreren möglichen Lösungen.

Erklärung

Erstellung des Konfliktgraphen

Um den Konfliktgraph bestimmen zu können, müssen normalerweise zuerst die Aktivitätsbereiche der Register bestimmt werden. In diesem Beispiel sind sie schon angegeben und daher verweise ich auf den entsprechenden Abschnitt in Beispiel 1 der Prüfung vom 15.3.96.

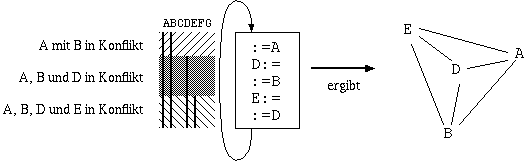
Der Konfliktgraph läßt sich nun ganz leicht aus den Aktivitätsbereichen ablesen: Sind zwei Register in einem Block zum gleichen Zeitpunkt aktiv, dann stehen sie miteinander in Konflikt. Zur Verdeutlichung hier noch einmal die genaue Vorgangsweise an zwei Beispielen:

Das macht man mit allen im Kontrollflußgraph vorkommenden Blöcken und bildet daraus den vollständigen Konfliktgraph.

Berechnung der Auslagerungskosten

Die Auslagerungskosten sind sehr einfach zu berechnen. Für jedes Register zählt man die Anzahl der Speicher- und Ladebefehle. Man beachte dabei die Ausführungshäufigkeiten, die neben den Blöcken stehen und multipliziere sie entsprechend. Die Anzahlen werden mit den entsprechenden Kosten der Zyklen multipliziert, in diesem Beispiel also mit 1 bzw. 2.

R| R:=| :=R|Summe
-+----+----+---------------
A|  5 | 10 | 25 =  5 + 10*2
B|  5 |  9 | 23 =  5 +  9*2
C|  5 |  1 |  7 =  5 +  1*2
D|  9 |  9 | 27 =  9 +  9*2
E| 11 |  5 | 21 = 11 +  5*2
F|  2 |  2 |  6 =  2 +  2*2
G|  2 |  2 |  6 =  2 +  2*2

Reihenfolge der Registerbelegung

Der Algorithmus zur Registerbelegung ist in Kapitel 8.3 des Skriptums beschrieben. Hier noch einmal eine Zusammenfassung:

1. Zuerst entfernt man die Knoten aus dem Konfliktgraph deren Grad kleiner als die Anzahl der vorhandenen Register ist.
2. Bleiben keine Knoten übrig dann ist man fertig und geht zum Punkt 5.
3. Jetzt sind nur noch Knoten mit Grad größer-gleich der Anzahl der vorhandenen Register übrig. Man entfernt den Knoten, dessen Register die niedrigste Priorität hat.
4. Sind jetzt wieder Knoten mit einem kleineren Grad vorhanden dann zurück zu Punkt 1, sonst zu Punkt 3.
5. Der Graph ist leer. Wir sind fertig. Die Registerbelegung entspricht der umgekehrten Reihenfolge des Entfernens.

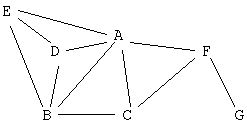
Hier ist noch einmal der Konfliktgraph. Eingezeichnet ist der Grad von jedem Knoten.

Wir können also zuerst nur das Register G aus dem Graph entfernen weil wir nur drei Register zur Verfügung haben. Der Graph sieht dann so aus:

Das nächste Register ist also F und danach C. Jetzt können wir kein Register mehr entfernen, weil der Grad an jedem Knoten überall drei ist.

Um herauszufinden welchen Knoten wir als nächsten entfernen dürfen, müssen wir die Prioritätsfunktion der übriggebliebenen Register berechnen. Sie ergibt die Werte:

p(A) = 25/3
p(B) = 23/3
p(D) = 27/3
p(E) = 21/3

Anmerkung: Für die Berechnung muß natürlich der aktuelle Grad des entsprechenden Knotens herangezogen werden!

Das Register E hat die geringste Priorität und wird daher ausgelagert. Wir können den Knoten E aus dem Graph entfernen und gelangen zu

Jeder Knoten hat einen geringeren Grad als die Anzahl der zur Verfügung stehenden Register. Die Knoten können daher in beliebiger Reihenfolge entfernt werden, z.B. zuerst D, dann B und zuletzt A. Es kann aber genausogut A, B, D oder B, A, D sein.

Die Reihenfolge der Registerbelegung entspricht der umgekehrten Reihenfolge des Entfernens der Knoten, also A, B, D, E, C, F, G wobei das Register E ausgelagert werden muß.

Registerzuteilgung auf reale Register

Bei der Registerzuteilung gehen wir wieder vom Konfliktgraph aus, wobei wir diesmal das Register E ignorieren, weil es ja ausgelagert ist und damit nicht in Konflikt mit einem Maschinenregister steht.

Anmerkung: Der Computer führt seine Berechnungen mit Hilfe eines Arbeitsregisters durch. Die Zuweisung E:= des Arbeitsregisters auf das Register E wird einfach durch ein store E ersetzt, d.h. der Inhalt des Arbeitsregisters wird in den Hauptspeicher ausgelagert. Es wird also kein zusätzliches Register E im Prozessor belegt. Ensprechend wird :=E durch load E ersetzt.

Die Reihenfolge der Registerzuteilung entspricht der Reihenfolge der Reihenfolge der Registerbelegung die wir vorhin erhalten haben (ohne E), also A, B, D, C, F, G. A erhält das Register 1, B bekommt 2 und für D und C bleiben daher nur jeweils das Register 3 übrig. Dadurch erhält F automatisch das Register 2 und G das Register 1.

Der Graph mit der Registerzuteilung sieht so aus: